如何提高示波器频域分析的能力?
了解了“为什么示波器没有取代频谱仪”的原因,那么有没有办法让示波器在频域分析上变得更强大、更实用些呢?下面就分别介绍几种目前示波器里常用的方法。
滤波
频谱仪通过各种模拟/数字滤波器将系统带宽限制在一个较窄的范围内从而提高信噪比,同样的思路当然也可以用于示波器。然而如果在示波器的模拟通道上人为引入一些模拟滤波器不但会增加成本,而且与示波器追求高带宽的初衷相违背。为了解决这一矛盾,可以在数字域进行滤波。当已知信号中心频率和带宽时,可以先将ADC采样后的数字信号下变频到基带(数字下变频DDC),然后通过数字滤波器滤除带外噪声。这时再进行FFT得到的频谱图底噪就会降低。
Overlap FFT
示波器频谱分析功能的初期做法就是将采集到的数字信号进行FFT后显示在屏幕上。这种简单粗暴的做法会导致下面一些问题。
首先,对于数字信号来说,离散傅里叶变换(DFT)是时域信号和频域信号连接的纽带。所谓DFT,就是将数字信号进行周期延拓后计算这个周期信号的离散傅里叶系数(DFS),而FFT只是一种计算DFS的快速算法。在这个过程中周期延拓有可能引入信号的不连续,从而导致产生新的频谱分量(频谱泄露)。如图1所示。
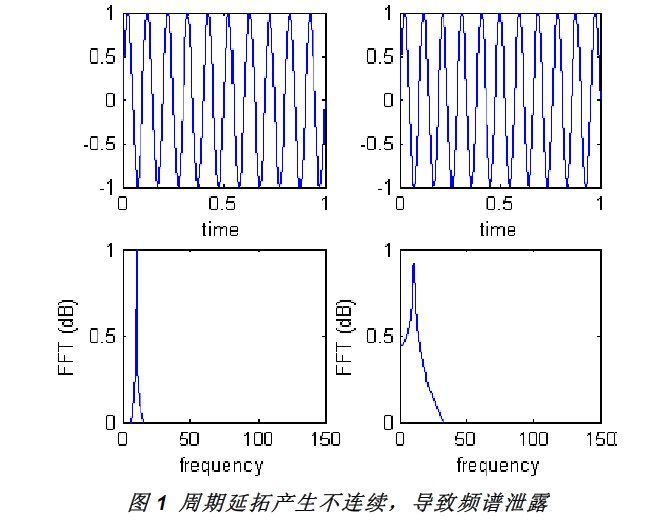
其次,FFT作为一种快速算法,要求样点个数满足2的幂次。同时,由于硬件实现时的资源限制,其FFT点数又不能太大,例如通常会采用2048点的FFT。然而示波器一次采集的样点数往往远大于FFT点数,处理这个问题有两种方式,1.不用FFT,直接计算DFT,显然这样会增加计算负担,导致响应速度、刷新率降低。2. 将较长的采集信号分成若干个2048点的小段,每段分别计算FFT。注意到第二种方式虽然计算量降低了,但仍然存在频谱泄露的问题。
为了解决这个问题,我们人为的将每个小段边缘的信号进行衰减,即加窗。这样信号周期延拓后就没有不连续问题了,频谱泄露问题得到了改善,如图2所示。
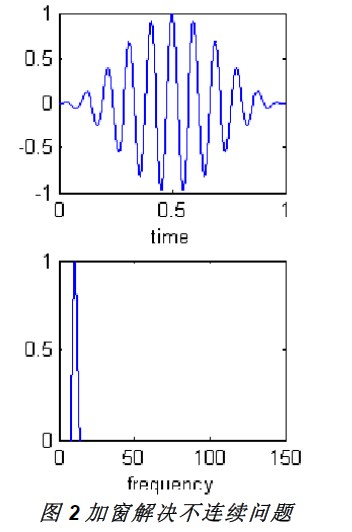
然而问题到此并没有完全解决,加窗就是给时域信号乘以一个窗函数,信号与系统理论告诉我们:时域的相乘就是频域的卷积。而窗函数的频谱显然不是一个Delta函数,卷积后原信号的频谱产生了弥散,因此窗函数的引入降低了频域的分辨率。人们又根据各种不同的准则设计出不同的窗函数,如图3所示。不同的窗函数其频域特征并不相同,有的关注于如何降低旁瓣电平(提高幅度分辨率,即让信号在噪声中浮出水面),有的关注于最小化主瓣宽度(提高频率分辨率,即让两个频域相邻信号在频域上分辨出来)。帕斯瓦尔定理说明时域或频域的能量是守恒的,要么把底噪压低些主瓣就变胖点,要么把主瓣挤瘦点底噪就抬高些。总之,鱼和熊掌不可兼得,表1提供了一些常用的窗函数供大家使用时参考。
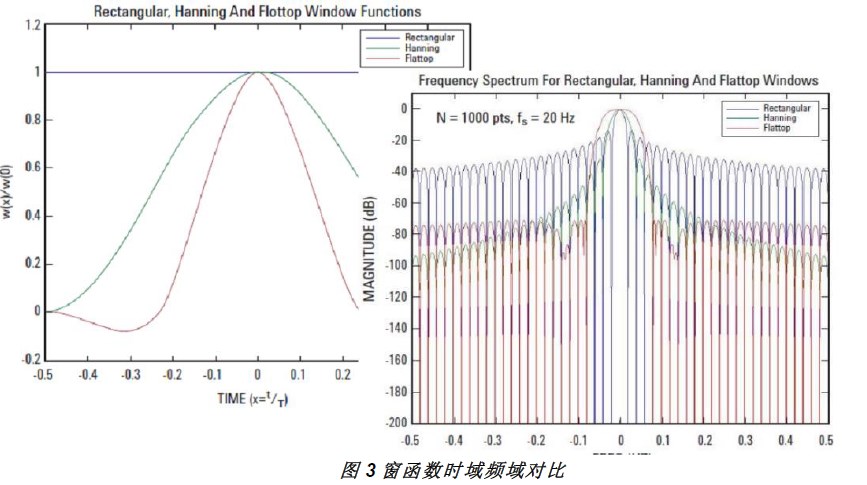
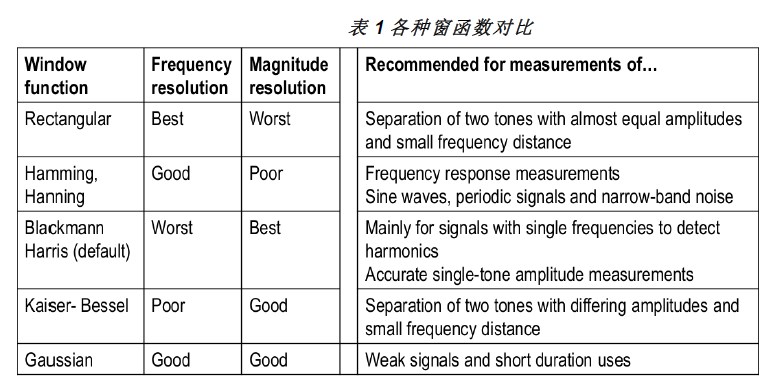
另外,对于时变信号,这种分段FFT的做法还可以带来另一个问题:有些瞬时出现的信号,很可能因为窗函数的引入而被衰减掉,无法在频域看到。解决方法也相当直观和有效,让每一段FFT之间有一段重叠(overlap FFT)。如图4所示。当然,这样做的代价是采样点被重复计算了,总的运算量增加了。
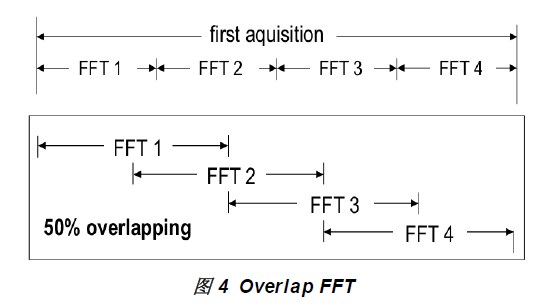
这里值得注意的是,不论加何种窗函数,是否overlap,分段FFT的方式相比直接计算DFT方式都会带来一个共同的问题:频率分辨率(RBW)降低。频域分辨率=采样率/DFT点数,分段计算减少了DFT点数,因此频域分辨率变差。
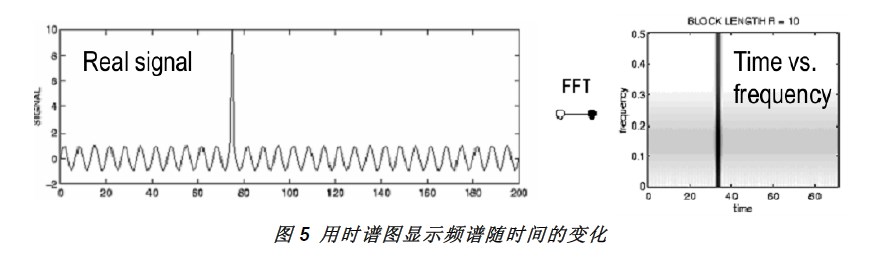
其实分段FFT的方式实际上就是时频分析中的短时傅里叶变换(STFT)。从这个角度讲,示波器还可以将时间轴引入画出一张频谱随时间变化而变化的时谱图。例如图5所示,通过观察时频域上的异常或许会更快的帮助我们找到问题之所在。当然,这种变换不仅限于STFT,还有Gabor变换等各种变换,就像窗函数一样满足不同的设计准则。此外,通过时频谱分析对于某些特定的调制信号,例如FSK、OFDM等,还可以设定特定的时频域触发条件(比如在时频谱上按时间依次画出f1,f2,f1,f3这样一个模板,当满足模板的pattern出现时示波器触发)。将现有一些示波器的频域触发功能扩展到时频域触发,这个功能在一些基带信号的调试过程中将起到很大帮助。
推荐查看:
版权声明:本资料属于北京海洋兴业科技股份有限公司所有,如需转载,请注明出处!




